文／蘇漢哲 新竹市育賢國中老師

《摘要》

這一堂探究式數學課，透過具體教具【起】【承】【轉】【合】的操作，讓學生玩懂抽象的三角形全等性質。

　　這是一堂數學素養課程，希望藉由學生自行探究，發展學生「三角形全等」的先備具體心像，奠定「三角形全等」的操作性幾何表徵心像，以利後續相關正式課程的進行。

一、設計理念

　　這份教案，是依據「十二年國教數學素養導向課程設計與教學案例」(單維彰, 鄭章華 主編) 所提六大素養導向設計原則編寫出來的。

(一)透過真實情境、寓言故事、數學史引入教材，營造數學學習需求:

　　例1:本教案運用生活情境中的咖啡杯蓋，以及心理學「賈斯特羅錯覺」來體驗視覺錯覺，進而強調需透過「完全疊合」才能驗證全等。

　　例2:本教案利用遊戲式情境「寓言故事--瑪利歐兄弟拯救公主」，攻擊三角形城堡拯救出公主，紀錄把六個物件(三個邊、三個角)由多到少逐步拆解的過程，三角形形狀何時無法維持(即剩下物件可以造出第二種(含)以上的三角形)[註1]，來探索出三角形形狀的不變性。

(二)以任務鋪陳數學學習脈絡，引導學生進行探索與發展概念:

　　由完全疊合，到三角形全等性質探究，都有一系列的任務活動。

(三)讓學生運用相關數學知識與能力解決問題，提出合理的觀點與他人溝通:

　　於遊戲中，三角形形狀是否改變，都需透過相關數學知識，提出合理的觀點與他人溝通。

(四)教材安排從具體到抽象，提供學生有感的學習機會。

圖一： 由具體的教具操作，到抽象的「全等性質」

圖二：探討「三角形全等性質」

圖三：體驗視覺錯覺，進而加強需透過「完全疊合」才能驗證全等。

(五)教材設計具備多重表徵(圖、表、文字、數字)

(1)由自製的「三角形扣條教具」，探討「三角形全等性質」。

(2)體驗「咖啡杯蓋「的視覺錯覺，進而對透過「完全疊合」才能驗證全等，更有需求性。

(3)「三角形移動方格教具」，體驗剛體運動的「平移」、「旋轉」、「翻轉」。

(六)學習任務具備形成性評量的功能，以評估與促進數學學習:

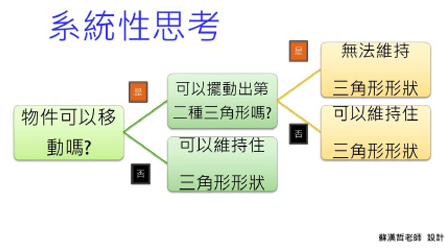
　　每一次的紀錄與判斷，與任務學習單都是形成性評量。三角形形狀有否改變成另一種三角形，學生可以建立系統性思考

1．當元件邊或角，不可以被移動，當然三角形保持形狀不變

2．當元件邊或角，可以移動，

(1)但一移動就無法構成另一個三角形，則三角形的形狀無法被改變

(2)移動後又可以構成另一個三角形，則三角形的形狀可以被改變

圖四: 系統性思維_21世紀八大核心技能 (批判思考、創造力、研究與探究、自主堅持、資訊使用、系統性思維、溝通、反思)

二、教學內容分析

1. 平常課本教學：

(1)給定三線段，利用尺規作圖，畫完後，宣告以SSS作圖法所作出的三角形都會一模一樣。

(2)以一三角形之透明片，使用尺規作圖畫出與此透明片三角形相同之三邊長，檢驗其是否重合。

2. 本教案課程設計特色：

　　本教案為遊戲式探究，教學脈絡具起、承、轉、合，並結合情境引入教材。不同於以往以尺規作圖，來教三角形全等，改以「遊戲式探究的方式」來讓學生自行發展與探究出三角形全等性質。

(1) 互相疊合:學生透過咖啡杯蓋的「賈斯特羅錯覺」發現要判斷杯蓋是否一樣，一定要透過「互相疊合」。

(2) 剛體運動:兩個三角形是否全等，要透過互相疊合，如何才能疊合?疊合前要透過平移、旋轉、翻轉等剛體運動。

(3) 建構相同的三角形城堡(由少的條件-->到多個條件):發現好像至少三個條件就可以建造同樣的三角形城堡。

(4) 三角形城堡是否被攻破(由多個條件-->到少的條件):發現至少要有三個條件，在某些組合下，可以維持住三角形城堡不被攻破(三角形形狀不變)。

讓學生自行實作、經歷、討論與推論出三角形全等性質。

三、大家一起來實作

(一)【起】完全疊合

　　利用咖啡杯蓋，產生的「賈斯特羅錯覺」，讓學生經驗視覺上所產生的錯覺，必須透過"互相疊合」來驗證，圖形是否全等。

圖五：運用賈斯特羅錯覺說明疊合的重要性。

(二)【承】要讓兩圖形完全疊合，疊合前必須透過剛體運動，引導出剛體運動的需求性:平移、旋轉、翻轉。

(三)【轉】如果不透過疊合的話，有沒有什麼辦法來判斷兩個三角形全等?引導出探討三角形全等性質的需求性。

◎由少到多，三角形有3個角3個邊，由一個物件開始逐步增加，遊戲式探究三角形全等性質

◎由多到少，三角形有3個角3個邊，由一個物件開始逐步減少，遊戲式探究三角形全等性質，並運用透明片或底板來疊合判斷，是否構成不一樣的三角形。

圖六： 學生使用遊戲化探究的歷程

(四)【合】請學生反思，分組討論與發表，維持住三角形形狀的最少條件。

(五)在這份教案中，我們同時訓練學生服膺廿一世紀的公民應該具備的八大核心技能，包括:

1．批判性思考:遊戲進行中或分組報告時，有人說這樣能維持住三角形的形狀，其他人可對他提出質疑。
2．創造力:在拆解三角形的過程中，會有不同的三角形擺動方式。
3．研究與探究:拆解三角形，解說維持住或無法維持住形狀，是一種探究的歷程。
4．自主與堅持:如何自主向同學說明自己的想法。
5．資訊使用:可用GGB幾何動畫說明。
6．系統性思維:如何判斷三角形的形狀是否改變，會逐步建立一種系統性的思維架構。
7．溝通:遊戲過程中，組內會不斷與同儕溝通討論，組間各組報告也是溝通的一種。
8．反思:在統整各小組的報告階段，會不斷與夥伴反思剛剛的遊戲歷程，由歷程中尋找維持住三角形的最少條件。

四、學習單的收斂與總結階段

(一)教師收斂統整，遊戲後引導提問、由學生發表或合作討論：

　　各組將討論結果寫在小白板，並貼在黑板上。發表正確組數越多每個10分，對別組挑錯的 (培養批判性思考，與反思能力) 每個20分，得分最高的組別為最後的大贏家。

圖七：學生上台說明ASA是全等性質	圖八：學生上台說明AAA非全等性質，因可以放大縮小

(二)師生共同反思遊戲式學習活動與情意交流

(三)書寫學習單

1．由以上遊戲討論中，可以診斷式教學，對於SSA，不成立的條件去做探討，學生手邊也有具體的三角形扣條可以操作。學生會發現鈍角、直角時都會全等，銳角有兩種情形，只有其中一種會不全等。

2．延伸引導，會發現AAS即為ASA，ASA即為AAS

圖九：邊邊角(SSA)是否為全等性質	圖十：邊邊角(SSA)藍邊可移動，構成另一個三角形，因此SSA非全等性質

教學反思

　　上完這套課程，我發現，孩子喜歡競賽遊戲，課堂反應很熱烈，但老師也要拿捏遊戲和講解的時間，才能達到好的學習效果。有人認為遊戲化學習，只有煙火沒有效果，是因為少了後續學習單的收斂與統整。而學生透過操作討論、反思回饋，所得到的三角形全等性質，會更有感覺，也記得更久。傳統教學上大多是直接給標準的完美答案，讓學生去記憶與熟練，但學生卻失去了從中探索的歷程與發現的樂趣，少了研究與探究、批判性思考、溝通與反思等能力。或許，當我們在設計課程時，能多思考透過真實情境引入數學教材，並用任務取向來鋪陳數學學習脈絡，學生更能在生活中運用數學知識展現解決問題的能力，也認同數學的有用性，這樣才是我們所期待的素養教育吧!